404

一个数X，0

1)16x是整数

2)8x是整数

(提供者ID：awei64。)

(1) 由于0

当n=1时，x=1/16=0.0625

当n=15时，x=15/160=0.9375

所以不能确定

(2) 由于0

当n=1时，x=1/8=0.125

当n=7时，x=7/8=0.875

小数点后一位不为0

所以选B

405

26除以k余数是k-2, k?

条件1: k<10

条件2：k>5

(提供者ID：jiahewang。条件里的数字不太确定，狗主选的C)

由题面可知，26+2(28)是K的倍数,。28的因子有1,2,4,7,14,28又因为余数为K-2,则K>2，K的可能值为4,7,14,28.

(1) K<10，K可能等于4或是7，不能确定

(2) K>5，K可能等于7,14,28，不能确定

同时满足(1)(2),5

选C

406

除以21,15,27余2的最小整数?

(提供者ID：jiahewang。)

说明这个数字减去2之后，是21(3*7),15(3*5),27(3*3*3)的最小公倍数，即 7*5*3*3*3+2=945+2=947

407

Gross profit 是cost的150%，售价65，求Gross profit?

(提供者ID：jiahewang。)

Price-cost=Gross Profit

65-cost=1.5 cost 推出cost=26

Gross profit=26*1.5=39

408

一个盒子有红铅笔和蓝铅笔，如果红的拿掉一只，和蓝铅笔一样多，如果蓝的拿掉一只，红的是蓝的的2倍，求铅笔总数

(提供者ID：千里殿下。)

设红铅笔为X只，蓝铅笔为Y只，根据题意，可列方程式：

X-1=Y

X=2(Y-1),解方程，得，X=4，Y=3

铅笔总数=x+y=7

409

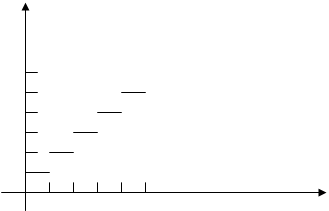
[X] is the integer greater or equal to x, ask x-[x]<0? (我记得好像是小于号)

(1) x is positive

(2) x is not a integer

(提供者ID：徐大喜。)

图片1

大致画了下[x]的函数图象，可以知道y=x的函数图象是一条斜率为45°的斜线。(1)当X为正数是，有图可知，只有当X为正数时，两条函数有交点。其他情况，x<[x] 不能确定

(2) x不为整数时，x的函数图象总在[x]的函数图象之下，即x<[x],x-[x]<0

选B

410

X>0 吗?

(1)X^3

(提供者ID：mrjihai。)

(1) 推出，X>1或X<0 不能确定

(2) 推出，0

选B

411

P

(1)T

(提供者ID：mrjihai。)

(1) 有可能，P

也有可能 S

S

(2)有可能 S

也有可能 S

(1)(2)，同时考虑， S

S

选E。

412

某地区进行一个试验，tried 2 classes in each 32 classes in different schools invloved 39 teachers. 每个老师最少教1门课，最多教3门课，如果m代表上3门课的个数，m的最小值和最大值是多少。前面部分的陈述和后面的关系我就没太弄懂。答案有 0和13，0和14，1 和9 等

(提供者ID：BananaPaper。)

413

KPNMQ是一条直线上的五个点。(可能字母记得不全对)求是否KN小于NQ?

1. PN小于MQ

2. KN小于MQ

(提供者ID：xuexixuexi1020。狗主选了B)

(1) 不确定KP和NM的大小关系，无法确定

(2) KN小于MQ，说明KN小于NM+MQ，所以KN小于NQ

选B

414

ABC为一个百位数的三个数字，ABC是否可以被9整除

1)A, B, C之和可以被3整除

2)A=C+3， B=C+3

(提供者ID：wbhsky。狗主不知道，可能是D吧~)

(1) 三个数字之和可以被三整除，只能证明ABC这个数字能被3整除，仅仅有能被9整除的可能性。

(2) 由条件可得，ABC三个数字之和为C+3+C+3+C=3C+6=3(C+2)

可以被3整除。当一个数的各位数字之和为9的倍数时，这个数字可以被9整除。3(C+2)不能肯定是否能被9整除。

选E

是JJ的变体，问一个3位数能否被3整除(JJ里是问能被9整除)?

(1)该3位数的各位数之和能被9整除

(2)该3位数的百位数和十位数相等且都等于个位数+3

(提供者ID：hxh2215。狗主选的D，解法和JJ里一样。)

(1) 三位数之和能被9整出，既也可以被3正处，所以这个三位数可以被3整除。

(2) ABC桑位数之和为C+3+C+3+C=3C+6可以被3整除，所以这个数可以被3整除。

选D

415

想了解一个区间内有几个整数

1)区间的一个端点是整数

2)区间的小的数比大的小9

(提供者ID：wbhsky。狗主选C~)

(1) 给出区间起点，但未确定区间范围，不能确定

(2) 如果起点为整数，比如1，大的数则为10，区间内的整数为10(inclusive)

如果起点不为整数，比如1.5，大的数则为10.5，区间内的整数为9(inclusive) 不能确定

同时考虑(1)(2)，可得区间内的整数为9(inclusive)

选C

416

版本一：-a

(1).a^2>a

(2).a^2+a is negative

(提供者ID：huikuicd。)

版本二：a and x are both real numbers. -a

条件1：a²-a>0

条件2：a²+a<0

(提供者ID：rachel910903。条件1算出来a>1 or a<0，不充分，条件2算出来-1a²了，那X就不存在了，狗主就不知道这种情况到底是充分还是不充分……题目楼主肯定没有记错，但就不知道中间到底是哪个想法出错了……)

-a-a，a≠0

(1)a²>a ，又a² >-a。推出a<-1或a>1.

如果a<-1，则-a1.

如果a>1，则-a

(2)a^2+a<0， a²<-a 又题面为a² >-a，矛盾。无法判断。

综合(1)(2)，不能确定x是否为正。

选E 

邮箱：
验证码：